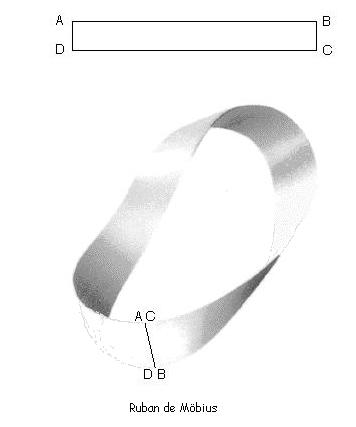
Sculptures de l'infini inspirées par le ruban de Möbius

Arts et mathématiques

Le ruban de Möbius, est une surface non orientable à deux dimensions avec seulement un bord quand elle est plongée dans un espace euclidien à trois dimensions. Cette surface découverte en 1858 par le mathématicien allemand August Ferdinand Möbius (1790-1868) a cette particularité de ne posséder qu'une seule face.

 Pour construire ce ruban, prenez un rectangle de papier, et coller les largeurs entre elles, mais en ayant fait tourner d'un tour votre rectangle.

Des variantes du ruban classique peuvent s'obtenir en faisant subir à la bande de papier un nombre impair de demi-tours de sens direct ou rétrograde

 

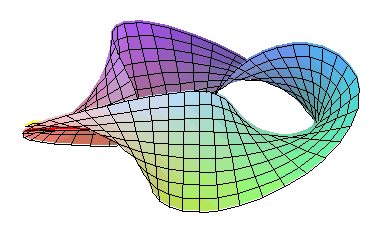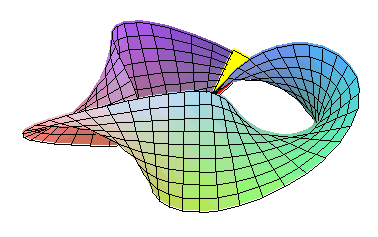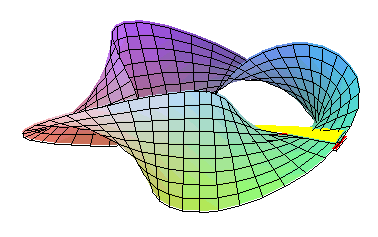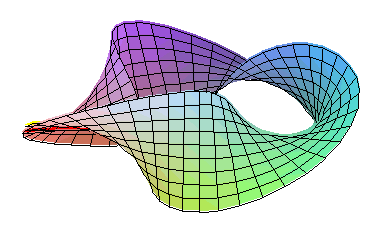
La bouteille de Klein est une surface non-orientable avec une seule face. Deux bandes de Möbius se trouvent sur sa surface le long de laquelle on peut se déplacer en continu à partir des deux côtés de la surface. Une deuxième bande de Möbius est de l'autre côté, symétrique de la bande montre.

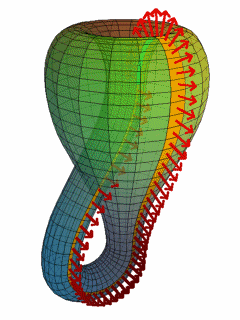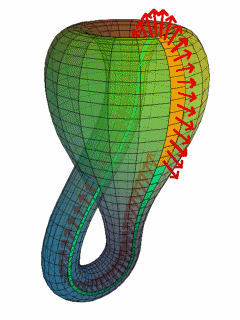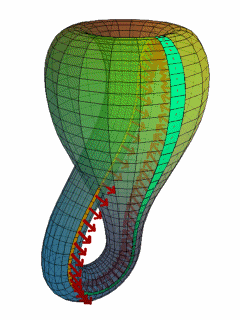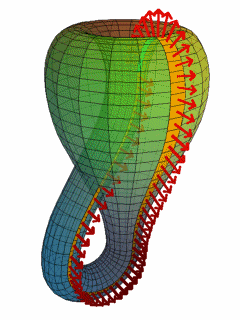
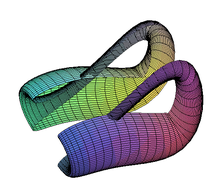
Le découpage d'une bouteille de Klein en deux moitiés le long de son plan de symétrie donne deux bandes de Möbius en miroir l'une par rapport à l'autre.

 

Ressources Internet :

Classification des sculptures mathématiques :

Aase Texmon Rygh

Möbius stående, 1995, bronze, Stavanger, Norvège

Marco Slinckaert

Le Serpent - Sculpture de la Solidarité à Lille - Wazemmes - France

Ce ruban de métal composé de 3000 pièces en acier inoxydable est inspiré du ruban de Möbius. Situé dans une fontaine de la Place De La Solidarité, du quartier Waremme à Lille. C'est l’œuvre déconcertante de l'artiste Lillois Marco Slinckaert. Longue de douze mètres pour sept de haut, faite de dix tonnes de métal, la sculpture est inaugurée en 1989 par le président François Mitterrand lui-même. « Aérienne, aquatique et semi-aquatique », telle que décrite par son créateur. Dès 1984, Marco Slinckaert a multiplié les études sur sinusoïdes. Aidé par Claude Baquet, chef d'atelier, il mettra deux ans pour réaliser son ruban d'acier , allégorie de la Solidarité , une chaîne sans fin qui rappelle le symbole de l'infini. Fabriquée en acier inoxydable, elle a été réalisée à Roubaix par Inoxi France.

Sur cette archive de l'INA, Marco SLINCKAERT explique qu'il travaille depuis plusieurs années sur les thèmes d'infinitude, de notre incapacité à la « mettre au réel » dans l'espace, le temps et les nombres. Tout comme la statue, la solidarité fait coexister des choses de nature différente.

Keizo Ushio

Ruban de Möbius, Granite, 2 mètres. (Mihama, Japon, 1990)

 

“Moebius in Space Planet”, à "Sculpture by the Sea" ( Bondi, Australie, 2011)

Max Bill

Max Bill - architecte, concepteur, peintre, sculpteur, commentateur et conférencier - défini l'art concret en étant finalement « l'expression pure des dimensions et des lois harmoniques » pour une approche mathématique de la conception créative afin de maintenir des résultats contrôlables. La découverte mathématique de la bande de Möbius, a intéressé Max Bill en tant que sculpteur pendant des années.

 

Kontinuität (Continuity), 1986, Deutsche Bank, Frankfurt am Main

 

Open air museum for sculpture, Middelheim Antwerp, "Endless twist", 1953-56

 

Doppelfläche mit sechs rechtwinkligen Ecken (double surface with six rectangular corners)” (1976)

 

Paul Griot

La sculpture est installée depuis 1967 sur le parvis de la faculté de Rennes (France). Inspiré du ruban du mathématicien Moebius, cette œuvre est composée de plaques de cuivre et de laiton sur une ossature métallique.


Robert R. Wilson

Au Fermilab, laboratoire de physique des hautes énergies aux USA. Le ruban de Möbius est monté au milieu d'un bassin circulaire au-dessus Auditorium Ramsey. Il est composé de 3 x 5 pouces morceaux d'acier inoxydable qui ont été soudés sur une forme tubulaire huit pieds de diamètre. Cette sculpture a été inaugurée en mai 1974.

Plamen Yourdanov

 

Double Mobius Strip, Chicago, USA,  2003

 

Double Mobius Strip, Chicago, USA, 2002

 

Jennifer Macklem et Kip Jones

Natural Language, Mobius strip sculpture (2000). Sculpture située à l'extérieur de la Bibliothèque publique de Kelowna, Canada

 

John Robinson

IMMORTALITY, "Passing on the Torch of Life", bronze, 1982

 

ETERNITY, Civic Centre, Pietre Place, Canberra, Australie, bronze, 1980

 

JOURNEY, Science and Technology Department, Macquarie University, North Ryde, Sydney, Australie, 1996

 

Vito Acconci

Mobius bench, Shops at Lake, Pasadena, USA

 

Fukuroi City, Japan 2000-2001, en fibre de verre translucide et lumières fluorescentes

 

Architecture

Le bâtiment CCTV à Pékin, le siège de la télévision centrale chinoise conçue par Rem Koolhaas et Ole Scheeren

 

 

The Klein Bottle House, par l'architecte McBride Charles Ryan, située à Rye, Australie

 

 

Projet en cours : L’agence d’architecture Danoise Big (Bjarke Ingels Group) a été choisie pour réaliser la future bibliothèque nationale d’Astana, capitale du Kazakhstan. D’une superficie de 33 000 m², elle aura la forme d’un ruban faisant un ample mouvement circulaire. Selon le directeur de l’agence BIG: « Sa forme, un ruban de Moebius, combine quatre archétypes universels et intemporels : le cercle, la rotonde, l’arche et la yourte ».
Le chef de projet de l’agence y va aussi de son commentaire: « L’enveloppe du bâtiment transcende les critères traditionnels de l’architecture, car le mur devient toit, puis sol, puis redevient mur, à la manière d’une yourte ».

 

Mathématiciens Sculpteurs

 

Par Helaman Ferguson, Torus Ombilic NC, 1988

 

 

Par Alex J. Feingold. Bande de Möbius en bronze, où la surface se reconnecte à elle-même après être passé par un trou dans la surface, 2008

 

 

Art graphique et impression 3 D

 

Moebius Ring 5, from jotero.com

 

Moebius Ring 6, from jotero.com

 

texture avec la figure géométrique Spidron réalisé avec k3dsurf et Paracloud

 

Klein Bottle and Trefoil-Knot (Sauermann Variant)

 

 

Sculpture moderne représentant deux rubans de Möbius imbriqués. Impression en 3 dimensions d'une sculpture moderne représentant une curiosité mathématique: deux rubans de Möbius imbriqués l'un dans l'autre (design organique). La complexité de cette sculpture rend impossible les opérations de moulage, seule l'impression 3D permet la réalisation de pièces aussi complexes.

 

Alan Bennett

Sculpture de verre pour le musée des sciences de Londres, 1995
Le souffleur de verre britannique Alan Bennett s'est spécialisé dans la conception de bouteilles de Klein emboitées.

 

La surface de Boy, un défi pour le sculpteur

La surface de Boy peut aussi être « vue » comme une sphère dont on a recollé deux à deux les points antipodaux, ou encore un disque dont on a recollé deux à deux les points diamétralement opposés de son bord. On peut également la construire en recollant le bord d'un disque sur le bord d'un ruban de Möbius.

 

On peut avoir trois rubans de möbius qui passent par le pôle.

 

De même, une bande équatoriale constitue également un ruban (triplement tordu) de Möbius


Construction à partir du ruban de Möbius, par J-P Petit :
"Dans le Topologicon on trouve un petit dessin animé, un "feuilletable", qui montre comment un ruban de Moebius à trois demi-tours peut se transformer en surface de Boy. L'avant-dernière image de la série qui suit montre cette surface, moins un disque. Il suffit de rajouter celui-ci pour compléter la surface à la dernière image de la série. Inversement, on pourrait partir du disque et le faire croître, en s'auto-traversant, jusqu'à ce qu'il se recolle sur ce ruban de Moebius à trois demi-tours, ce qui est une autre construction."

Construction à partir d'un disque (source wikipédia)  : Pour obtenir la surface de Boy à partir d'un disque, on considère la circonférence de ce dernier qu'on replie sur elle-même de façon à lui faire effectuer un double tour. Les points qui étaient diamétralement opposés dans la circonférence initiale se trouvent alors en contact. On obtient ainsi une représentation du plan projectif et donc de la surface de Boy. Pour y parvenir, la surface doit nécessairement se traverser.

 

Max Sauze. Surface de Boy - Objets Topologiques, avec les scientifiques Bernard Morin et J.P. Petit. 1980-2000

 

Surface de Boy en métal ajouré (Mathematisches Forschungsinstitut Oberwolfach)

 

Surface de Boy, François Apéry